ABSTRACT

Analysis and synthesis of transitions between musical notes are open-ended problems in computer music. While much research has been done on the proper analysis and synthesis of musical timbres, less attention has been paid to what occurs between successively played notes. Using the Lemur representation, we have developed a graphical editor, LemurEdit, for closely examining and modifying analyses of violin transitions. A library of transitions components, indexed by their distinguishing characteristics, can be created for later recall in a real-time performance situation. These components are manipulated, joined, and finally synthesized to create any transition, as needed by the performer.

ACKNOWLEDGEMENTS

The author would like to thank everyone in the CERL Sound Group for their continued support in this ongoing research: Kurt Hebel and Carla Scaletti, for being excellent role models in the field of computer music (and probably the smartest people the author has ever met), Kelly Fitz and Bill Walker, two excellent programmers who gave the author many helpful hints and ideas when writing LemurEdit, and finally Professor Lippold Haken, more than just an advisor, but a true friend without whom none of this work could have been possible. His insight into the computer music field is unmatched.

1. INTRODUCTION

1.1. Definitions

According to Strawn [1], a transition "...includes the ending part of the decay [or release] of one note, the beginning and possibly all of the attack of the next note, and whatever connects the two notes." Transitions are typically on the order of 10-100 ms, and include a change in pitch, amplitude, and spectrum. Throughout this thesis, the transition region will refer to this period in time, and transition components will refer to the different parts found within the transition region. In the broadest sense, any kind of movement between one steady-state sound (including silence) to another constitutes a transition.

There are many different types of transitions between notes, even when considering only one instrument. Dynamics are of concern when characterizing transitions, e.g., the first note could be quiet, the second loud, and the pitch interval between the two notes is relevant. In the case of a violin, one must also consider bow pressure, bow speed, bow location, and pitch.

1.2. Psychoacoustic Importance Of Transitions

Psychoacoustic research [2] has shown that understanding speech is dependent on discerning the transition between two steady-state sounds, i.e., transitions between vowels. Some speech synthesis techniques, such as diphone synthesis [3], have taken advantage of this by weighting the error metric more towards accurately synthesizing all legal pairs of phonemes and their transitions, rather than vowels. Since transitions between musical notes are somewhat analogous to transitions between steady-state sounds found in speech, transitions seem worthy of analysis.

Also, research [4] has shown that when a subject is identifying musical instruments, given only short examples of the timbre (e.g., just the attack, sustain, or release), the attack had the greatest influence on the subject's decision. This implies that transitions between steady states may provide important cues that should be synthesized accurately.

1.3. Transition Processing

1.3.1. Simple transition processing

Sampling synthesizers employ simple transition processing. Typically, a cross-fading technique is used to overlap the release of the first note and the attack of the second. Likewise, FM synthesizers perform simple transition processing with cross-fading [5]. Portamento is sometimes used in synthesizers as a form of transition. As the second note begins, the pitch and amplitude of the first raise (or lower) to meet the pitch of the second. Unfortunately, sometimes this technique is used where portamento is not a recognized characteristic of the instrument. Portamento is most suitable for playing glissandos.

1.3.2. Transitions in physical modeling

In physical modeling [6], transitions are inherently a part of the model. Since synthesis of physical models accounts for the actual physical characteristics of the instrument, transitions will be synthesized accurately if the model itself is accurate.

1.3.3. Transitions in sinusoidal models

James Beauchamp analyzed transitions using the pitch-tracking heterodyne filter [7], [8]. However, this technique assumes that only one note is playing at a time, and there is no temporal overlap. Since the heterodyne filter technique requires small variations in the interval between the two notes, either two separate analyses have to be made for each note, or the transition must be constrained by a small pitch interval. Strawn [9] analyzed and synthesized musical transitions using the Phase-Vocoder, a pitch-tracking technique related to the heterodyne filter but based on the Discrete Short-Time Fourier Transform. Two separate analyses were made: one of the first note, and one of the second. At synthesis time, cross-fading between the two syntheses was used to simulate the transition. Strawn suggests that it would be interesting to perform the same research using the McAulay-Quatieri technique presented in [10]. In this thesis, we have taken his advice.

1.4. A New Approach to Transition Synthesis

We model the transition region as a rather complex moment in time when the first note ends in a manner different from a normal release, and the second note overlaps it and begins in a manner different from a normal attack. As a result, we have developed a new technique for synthesizing transitions in real time. First, we analyzed many different transition types for a given instrument. Transition components are stored in a library indexed by parameters characteristic of the instrument to be synthesized. At performance time, when a transition is required, the appropriate transition is requested of the library and synthesized according to the demands of the performer. Additive synthesis on the Capybara Signal Processor is used at performance time to sum the sinusoidal components of the instrument in question. Chapter 2 of this thesis discusses the fundamentals behind the analysis method used and why it was chosen. Chapter 3 is a description of the graphical editing tool designed for the research presented herein. Chapter 4 is an analysis of the findings achieved by closely examining these transitions with our newly developed tool, and Chapter 5 discusses the library and its implementation.

2. A SINUSOIDAL ANALYSIS/SYNTHESIS MODEL

2.1. The McAulay-Quatieri Technique

Our analyses use an extended McAulay-Quatieri (MQ) sinusoidal technique. The MQ technique (originally described in [10]) models sounds as sinusoids with time-varying amplitudes and frequencies. Overlapping blocks of samples are successively passed to a Fast-Fourier Transform (FFT). The input to each FFT is windowed using a Kaiser window with an adjustable main-lobe width and side-lobe height, and is zero-padded to twice the length of the input. "Peaks" (or sinusoids) in the resulting spectrum are isolated using parabolic interpolation. These peaks then constitute the sinusoids within a "Frame" (or number of samples between successive hops of the window over the sampled data). Peaks are then matched between frames constrained by a maximum- (or minimum-) allowed frequency drift. The joining of peaks over time is called a track, representing a sinusoid with a time-varying amplitude and frequency. Tracks have the ability to be "born" and to "die," depending on whether the current peak is above or below a prescribed analysis threshold. A full analysis is a file showing the spectral evolution of a sound, where time is divided into frames, and each frame consists of a number of peaks representing sinusoids with an "instantaneous" amplitude and frequency in that frame. A more extensive explanation can be found in [10], [11] and [12]. Figure 2.1 is a block diagram illustrating the MQ technique.

2.2. Lemur: An Applied Extension to the MQ Technique

The MQ technique was implemented by Maher [14], [15], and later modified as Lemur [12], an application written for the Macintosh(TM) by Kelly Fitz and Bill Walker at the CERL Sound Group. First, they added the notion of frequency bins to account for the psychoacoustic masking properties of the human ear.

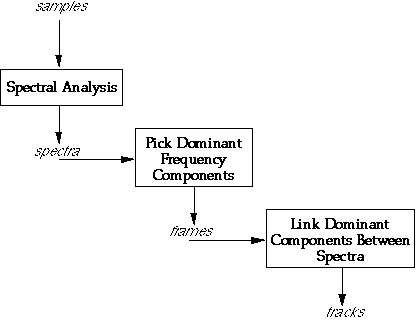
Figure 2.1: A track represents the time-varying frequency and amplitude of a single-frequency component in the analyzed sound [11].

Figure 2.2 illustrates how a loud tone can mask nearby ones with lower amplitudes. For example, if one listens to a 415 Hz sinusoid at 0 dB, summed with an 800 Hz sinusoid at -30 dB, a listener may not perceive the higher-pitched frequency. However, if the two sinusoids were kept at the same amplitude but the 800 Hz sinusoid moved to 4000 Hz, a listener would perceive both sinusoids. This is a psychoacoustic effect called masking.

In the original MQ technique, one global threshold parameter (or noise floor) is used across the entire spectrum in each frame of the analysis. Any peaks found below this threshold are assumed to be noise and not included in the

Figure 2.2 [Currently not available]: Masking levels corresponding to a 415Hz sinusoid [13].

construction of the current frame. There also exists a local threshold that is applied individually to base-two logarithmic sections of the total spectrum. Peaks found below the highest peak's amplitude (in that frequency bin) minus the local threshold are thrown out. From the previous example, let us assume that the local threshold for each bin is 20 dB. The 800 Hz sinusoid at -30 dB would be thrown out due to the amplitude of the 415 Hz peak, assuming that both peaks were within the same frequency bin. However, if the loudest peak in the bin containing 4000 Hz was at - 15 dB, the 4000 Hz, - 30 dB sinusoid would be kept. This extension roughly simulates masking properties occurring in the ear.

Fitz and Walker also extended the MQ algorithm with hysteresis. An effect affectionately dubbed the "doodley-doo" effect by James Beauchamp was discovered when certain thresholds were crossed multiple times by a sinusoid with a time-varying amplitude (or amplitude modulation). This is most evident in harmonic sounds with amplitude vibrato. At a high point in the sinusoid's amplitude, the signal would cross over the threshold and be included in that frame's list of peaks. At a low point, the sinusoid's amplitude drops below the threshold, and the peak is thrown out. Figure 2.3 shows a time-frequency plot of this artifact. After synthesis, the rapid turning-on and -off of the sinusoid is quite audible and undesirable.

Figure 2.3: Example of the "doodley-doo" effect. Notice the disappearance and reappearance of the partial at ~ 4400 Hz and ~5000 Hz.

To solve this problem, the analysis hysteresis is a third threshold setting available in Lemur. Hysteresis allows tracks to drop a specified amount below the local frequency-bin threshold for any length of time. If the track rises above the threshold, it continues as before. If the track falls below the allowed local threshold minus the hysteresis, it dies. For example, if a sinusoid with -20 dB amplitude and +/-3 dB of amplitude vibrato is analyzed with a -22 dB threshold and 5 dB of hysteresis, the track would not die even though it traveled below the local threshold. If, however, the track's overall amplitude dropped to -24 dB, the track would be continuously reborn and forced to die on each cycle of the vibrato. Knowing this, one must choose the hysteresis parameter carefully, possibly to account for all harmonic instances of amplitude vibrato.

2.3. Modifying The Lemur Time-Frequency Representation

The Lemur representation, like other time-frequency analysis techniques, can pitch-shift a particular harmonic by multiplying each frequency of each peak in a track by a fixed constant. Frequency shifting is similarly done by adding a constant to all frequencies of each peak in a track. Time scaling is also simplified using a time-frequency representation. At synthesis time, extra samples are computed for each frame.

Not all analysis modifications correspond to actual differences in playing the instrument. In a frequency scaling or frequency shifting scenario, one must consider the instrument's characteristic frequency response. If one were to multiply the frequency of each harmonic by two, the amplitudes of each harmonic would stay the same. This is misleading since the actual response of the instrument has not been shifted higher in frequency by a factor of two. In other words, scaling all harmonics by some factor does not necessarily imply changing the pitch by the same amount. On a real instrument, playing one note, and then another, one octave higher, does not shift the frequency response of the instrument. In sum, playing two notes an octave apart corresponds to a change in timbre, as well as a change in pitch. This does not mean that we cannot perform slight modifications, but it does mean that we must consider such factors before performing certain modifications in the time-frequency domain.[1]

2.4. Why Use Lemur for Transitions?

Lemur has good properties for analyzing transitions. Previous analysis techniques assumed the presence of a single fundamental, using a window about the length of two full periods of the fundamental. The McAulay-Quatieri technique uses a very large window size, typically on the order of 3 ms. As a result, each spectrum has been smoothed out, where the sinusoids present in the signal are represented by peaks. Still, these peaks can be isolated and added to the current frame as sinusoids present in the signal at that point in time. Therefore, this analysis method can easily track changes in frequency and track several simultaneous fundamentals, which is of utmost importance when analyzing transitions in musical notes. In Strawn's work [9], two analyses were performed, each centered around the fundamentals of both notes. Using Lemur, it suffices to make only one analysis of both notes and their transition for close examination.

3. LEMUREDIT: A NEW GRAPHICAL EDITING
TOOL FOR LEMUR ANALYSES

To assist our transition research, we wrote LemurEdit, a graphical editing tool for Lemur analyses. Both programs are available via anonymous ftp to "unicorn.cerl.uiuc.edu" in the "/pub/lemur" directory. The distribution manual for LemurEdit is shown in Appendix A. This tool allows one to examine closely an analysis created by Lemur. We can "zoom in" on specific portions of graphs, save user-selected portions of graphs, delete tracks, cut out portions of time, connect erroneously unconnected tracks, and otherwise modify and "correct" analyses. Using the Lemur file format, algorithmically constructed analyses can also be created for later synthesis.

3.1. WindowSets

WindowSets are an advanced data type for representing Lemur analyses and its graphs on the Macintosh. The WindowSet is the basic structure for manipulating analysis files created by Lemur. The complete WindowSet structure can be found in Table B.1. LemurEdit can have multiple analyses open at once, and each WindowSet can have any number of LemurWindows (or views of the currently opened analysis.) The LemurWindow is another structure representing each view of its parent WindowSet on the screen. Each LemurWindow contains data specifying the region of the analysis being viewed, its size on the screen, as well as other Macintosh-specific parameters. The LemurWindow structure is shown in Table B.2.

3.2. Viewing Lemur Analysis Files

LemurEdit is different from other graphical time-frequency displays in that more emphasis is put on the time-frequency relationship, rather than on the harmonic amplitude-time relationship. Many time-frequency plots in computer music came from analysis methods that assumed that the signal was harmonic and, therefore, could center frequency bands around the fundamental and multiples thereof. Figure 3.1 shows a typical time-frequency plot from one such analysis method. Lemur works on a much broader class of signals; it does not require any knowledge of the fundamental of the input signal. Therefore, input signals can be enharmonic, and the resulting classical time-frequency plots are hard to read. Figure 3.2 is a typical graph shown within LemurEdit, demonstrating the philosophy behind emphasizing frequency vs. time, instead of harmonic amplitude vs. time. LemurEdit allows the user to examine closely analysis files with its "zoom" feature. The user performs a click-and-drag operation to highlight a particular region of interest within the analysis. A keystroke will create and draw a new LemurWindow showing just that selected region. There is no limitation on the resolution in the vertical direction, since frequency lies along a continuum. However, since time is quantized into frames, the horizontal resolution is limited to the length of a frame.

3.3. Time Cutting

Time cutting allows the user to remove an integer number of frames from an analysis. After all of the selected frames have been removed, the next step is to rejoin tracks on each side of the cut. This is much like Lemur's analysis procedure where peaks in adjacent frames are connected to form sinusoidal tracks. The frequency drift parameter of the original analysis determines which tracks on one side can be rejoined with certain tracks on the other. Finally, any unmatched track ends are given birth- or death-peaks on the corresponding side of the cut.

Figure 3.1 [Currently not available]: A typical time-frequency plot generated by a harmonic analysis technique [17].

Figure 3.2: A typical LemurEdit graph. Pertinent analysis parameters are visible at the bottom of the graph; peak data at the top of the graph are updated dynamically given the current cursor location.

3.4. Saving Selected Tracks

This feature is useful for extracting specific components from an analysis. After selecting tracks of interest, one can generate a new analysis file containing only those tracks selected. This feature is extremely useful for separating the two notes when analyzing transitions. Other applications include listening to specific harmonics within an analysis, or extracting just the noise (typically represented by tracks of only a few frames in length) within the original signal.

3.5. Connecting Tracks

LemurEdit can connect two selected tracks. First, the death of the first track and the birth of the second are deleted from the corresponding frame structure. Second, peaks are inserted into the frames between the two tracks with linearly interpolated amplitude, frequency, and interpolated-frequency values. Before track connection begins, we must consider two things: First, it does not make sense to connect tracks that overlap. The user must be notified if this is attempted. There is an exception to this rule: if the death of the first track and the birth of the second track happen to lie in the same frame, track-connection is plausible. The birth- and the death-peaks are deleted, and the two ends joined. Second, there should be a limit on the change in frequency between the two tracks to be joined. If the allowed frequency drift of the analysis is 2%, we would not want to connect tracks 4% apart in frequency. LemurEdit does allow the user to do this, following a warning message.

3.6. Real-Time Feedback

Using the Sum-Of-Sines (SOS) program on the Capybara Signal Processor, the user can select individual tracks or entire regions and synthesize them in real time. Lippold Haken developed an additive synthesis engine using the Capybara Signal Processor developed by Symbolic Sound Corporation. It generates sinusoids using 72 low-frequency and 24 high-frequency oscillators. Each oscillator's amplitude- and frequency-envelope can be controlled independently, usually from a table of preloaded values. Time is represented by successive locations in memory, so that the amplitude and frequency of each oscillator is set by whatever location in memory is currently being accessed. Normally time is represented as a ramp function, meaning that memory is accessed sequentially and at uniform intervals. However, this is not mandatory. Any function for "time" can be used.

Altering the slope of the ramp function can either stretch or shrink the duration of the sound being synthesized without invariably introducing the "chipmunk" effect into the sound. This occurs because we are shrinking (or stretching) the duration of each harmonic in the frequency domain, instead of shrinking (or stretching) the entire time-domain signal. A negative slope will cause the sound being synthesized to play backwards. For an interesting effect, a sine wave will cause the sound to move backwards and forwards at varying speeds.

When we synthesize, first an analysis of a sound must be made using Lemur. Then the file is saved in a special format called an SOS analysis file. This contains all the information for each oscillator, such as when to turn on and off, what the amplitude is at each frame, and what the frequency is at each frame. Given the limited number of oscillators, more psychoacoustic processing is done to reduce the amount of data present in the analysis. The SOS Program, SOS Analysis File, and time function are loaded into the Capybara. Finally, a sophisticated protocol is used to tell the Capybara when to start playing the sound from the Macintosh. The protocol also allows the user to access memory directly within the Capybara. This is useful for changing the amplitude and frequency envelopes while the SOS analysis file is still in memory.

Once an analysis and its corresponding SOS equivalent have been loaded into the Macintosh and the Capybara, respectively, we can choose the portions of the analysis we would like to hear. This is done by sending a series of messages to the Capybara from the Macintosh that invert the amplitude envelopes of the tracks we wish to mute. Whenever the SOS program comes across a peak in a track with a negative amplitude, it turns off that track's oscillator. This feature allows the user to listen to individual harmonics, perhaps a combination of specified harmonics, or even tracks of a given length. In our transition research, we found it invaluable for listening to what we refer to as "lingering tracks": harmonics that do not die instantly once the transition region has been reached, but continue onwards for as long as 300 ms in some cases.

4. INVESTIGATION INTO TRANSITIONS

We now have the tools to build our library for performing sophisticated transition processing. Lemur and LemurEdit can be used to create sinusoidal analyses of transitions, to examine them closely , and to extract necessary components for insertion into our library. What follows are some conclusions made from examining the graphs of the analyses.

4.1. Some Recordings

Two sets of 16 digital recordings (Sets A and B) were made of different kinds of violin transitions. These recordings were performed by Katherine Kim in the Green Room of the Music Building Auditorium at the University of Illinois. Professor Lippold Haken recorded her performance onto Digital Audio Tape (DAT). Ms. Kim played all of the notes in less than ten minutes, on one violin. It was very important to maintain atmospheric continuity between each of the transitions. The transitions included ascending half steps, descending half steps, ascending whole steps, and descending whole steps. Some had vibrato, others had notes on open vs. fingered strings, and they varied in length. The recordings were later transferred from DAT to the Macintosh, and finally analyzed using Lemur. The following analysis parameters were used: a -70 dB noise floor, a 15 dB local threshold, 15 dB of hysteresis, and a 2% allowed frequency drift. A graph of each analysis, including a short description of the transition, is shown in Appendix C. A recording of these transitions is available on request.

4.2. Need for Special Transition Processing

An important question when considering transition synthesis is whether any special processing is necessary. Is a simple cross-fading technique suitable? Can we simply append a synthesized release for the first note, and a synthesized attack for the second note, merge the two, and call that a transition? Our research shows that cross-fading is too simplistic. Consider, for example, the transition shown in Figure C.1. Here we can see that the upper harmonics slowly fade in over the course of the attack of the first note. At the transition region, all harmonics are present as we move from the first note to the second. Likewise, the release shows an early fade-out of upper harmonics, while the release of the first note into the transition shows no such decay. This suggests that there really is a difference between transitions and steady-state attacks from silence (or steady-state releases into silence). Since the library will be used solely for transition processing, it must include components for transition attacks and transition releases. We can omit attacks and releases from silence, since that problem has been adequately solved with conventional synthesis techniques. Clearly there has to be a time threshold between when our algorithm determines whether we need special transition processing or whether a simple attack/release can be used. This thesis focuses on transitions between two steady-state notes, rather than transitions between silence and a steady-state note.

4.3. Harmonics in the Transition Region

We have identified three distinct types of behavior between the harmonics of the two steady-state notes within the transition region. All three are shown in Figure 4.1.

Transition Type #1: We found this type of transition to be the most characteristic of harmonic behavior within the transition region. The death

of the first track occurs two to three frames later in time than the birth of the second. Two oscillators are required to synthesize this partial.

Figure 4.1: Three types of harmonic behavior across the transition region.

Transition Type #2: This is a Lemur artifact, and presumed not to be characteristic of transitions. The two tracks spanning the transition region lie within the allowed frequency drift of the specified analysis parameters causing Lemur to connect the two tracks. At synthesis time, only one oscillator will be necessary to synthesize this portion. This transition type typically occurs when harmonics between the two notes coincidentally line up. Numerous examples of this can be seen in the analyses shown in Appendix C. For example, most of the half step transitions resulted in the connection of the fundamentals of both notes. This artifact can also occur for higher harmonics. In Figure C.6, we see the 9th harmonic of the first note connected with the 8th harmonic of the second. This poses a small problem when creating the library, which will be dealt with in Section 5.2.

Transition Type #3: This is a special case of type #1. Here the death of the first track and the birth of the second occur within the same frame, and again, two oscillators are necessary to synthesize this partial. It was speculated in [9] that such a discontinuity in frequency would result in "chirps." Further research showed that this is not the case since the amplitudes ramp up and ramp down; they do not cut off abruptly.

4.4. Length of Transition Region

How do we decide on the length of the transition region? Figure C.6 is a good example of a transition region that is clearly on the order of 300 ms. Figure 4.2 shows a close-up of the first five harmonics. Lingering tracks are almost always found where the first note was played on an open-string (See Figures C.8, C.9, C.24, C.25,) although they are most certainly not excluded to this type. Most of the half step interval transitions tend not to have lingering tracks, although this state may be a continued artifact of Lemur joining tracks across the transition region. Lingering tracks are more common among higher-intervaled transitions (See Figures C.6, C.7, C.22, C.23.) Still, we agree

Figure 4.2: Close-up of first five harmonics of Figure C.6. Notice the lingering tracks of the second and fifth harmonics of the first note.

that lingering tracks are typical of transitions. We can look at the higher harmonics of half step transitions and notice that as the corresponding harmonics drift further apart, lingering tracks start to reappear. (See harmonic #6 of Figure C.16.)

4.5. Transitions vs. Attacks and Releases

Transition attacks and releases are quite different from their regular attack/release counterparts. If one examines the release of the second note in Figure C.17, one sees that the harmonics tend to die out, one after the other. On the other hand, the transition release does not exhibit the same property. All of the harmonics exist at approximately the same amplitude throughout the duration of the sound, even into the transition region where they are abruptly cut off.

Likewise, the attack shows the first seven harmonics beginning together, while higher harmonics gradually fade into existence. At the transition attack, however, all the harmonics are present immediately at the beginning, which further supports our need to employ special transition processing.

5. THE LIBRARY

5.1. What Does the Library Contain?

We will concern ourselves only with transition attacks and releases between steady-state notes. Attacks from (and releases into) silence have been rigorously dealt with through alternative synthesis techniques. Our transitions are indexed by amplitude, interval, and bow change or no-bow change. It is important that we provide a sufficient representation of the possible transitions for a given instrument. Not including enough representatives can lead to an effect known as "electronic monotony." Consider Figures C.10 and C.11, two transitions that were played from the same note, had the same half step interval (from a B to a C), were played at approximately the same loudness, and were played with bow change. Looking carefully one will notice some differences. For example, there appears to be a strange track located between the second and third harmonics of the second note of Figure C.11. Should this be included as a part of the transition? There is a similar track located between the sixth and seventh harmonics as well; this one is of even greater length than the previous one. In Figure C.10, we see a lingering track located between the fifth and sixth harmonics of the second note. It is also approximately the same length as the longer of the two unidentified tracks found in Figure C.11. Maintaining these nuances can prevent electronic monotony. An experienced violinist will tell you that the transition in Figure C.10 has a smooth bow change, while the transition in Figure C.11 has a marcato bow change.

Clearly, the larger the library, the better the synthesis. Using the transition in Figure C.10 as an example, we have an analysis 188 kbytes in length, containing 816 frames. If we use all lingering tracks within the analysis, we must store approximately 80 frames of data, or ~20 kbytes of data per transition. For today's computer systems, it is not inconceivable to be able to store hundreds of transitions for a given instrument. With this in mind, it makes sense to include both transitions shown in Figures C.10 and C.11 in our library.

5.2. Building the Library

We use LemurEdit to extract the transition region present between the two steady-state notes. The first step is to separate the two notes. This can be done by selecting only those tracks that lie to the left of the transition region. A new analysis-file of the same length (in time) is created with only the first-note tracks. Likewise, another analysis-file consisting of just the second note

Figure 5.1: First note of the transition from Figure C.9. Notice the need to time-cut harmonics #9 and other higher-frequency ones. Harmonics #4 and #5 are lingering tracks (they belong to the transition release of the first note), and should not be time-cut.

Figure 5.2: Second note of Transition #A9.

is created. See Figure 5.1 and Figure 5.2 for an example of the separation of the transition. Occasionally, there are cases in which a harmonic from the first note erroneously connects with a harmonic from the second note, e.g., Transition Type #1 in Section 4.1. In this case, the offending track is included in both the first- and second-note analyses. A time-cut operation is used to remove the unwanted portion. The final step is to remove the steady-state portions of the first and second notes. This requires some careful consideration as to when the transition region begins and ends.

Another consideration is what to do with noise tracks. These are tracks that can be characterized by short lengths at typically low amplitudes. If one examines any of the transition pictures found in Appendix C, one will see that they can be found at the beginning of sounds (i.e., when the first note is being played), and at frequencies under ~200 Hz. Noise tracks found within the transition region are kept along with the transition components as they are extracted from the analyses. After the transition region has been chosen, any noise track whose birth is found to the left of the transition region median is assigned to the first note, while any noise track found to the right of the transition region median is assigned to the second. Noise tracks found below the fundamental are omitted altogether. They are considered characteristic of the instrument as a whole and should be synthesized separately. They are not to be included in the transition processing step.

5.3. Using the Library at Synthesis-Time

In a performance, our algorithm monitors the performer closely. When a note is released, it is up to the algorithm to determine whether a certain time-threshold has been reached. If the threshold is surpassed, transition processing is not needed, and a simple release is synthesized using any appropriate synthesis method. However, if another note is played before the

threshold, transition processing occurs, and we ask the library for a transition release for the first note and a transition attack for the second. The library will either return a "hit" or a "miss," given the parameters specified by the performer.

A library "hit" implies that a transition meeting the performer's requests is available for immediate synthesis. In this case, the transition release is recalled and synthesized in real time using the additive synthesis SOS program, running on the Capybara Signal Processor. If the library reports a "miss," the algorithm must find the closest transition in the library and synthesize it using interpolation to match the transition with what was requested by the performer. If the pitch is not close enough, we use Lemur to perform frequency scaling. If the amplitude is not right, simple scaling of each peak's amplitude occurs. These two parameters (in the case of our violin transitions) are the easiest values to interpolate, since they require little processing. Other parameters, such as bow change vs. no-bow change are more difficult, so it makes sense to include more varieties of transition attacks and releases with respect to that parameter in the library.

6. CONCLUSIONS

It is clear that synthesizers today (possibly with the exception of new physical modeling ones) pay little or no attention to transitions between musical notes. Transitions are complex, and a great deal of attention must be paid to the instrument in question. We have shown that, in the case of violins, special conditions exist within the transition region of two notes being played successively, which cannot be synthesized with simple cross-fading. In fact, there exist temporal overlaps in the harmonics between the two notes. Given a particular instrument, we can extract different transition types corresponding to different ways to play two successive notes. These transition components can be incorporated into a library of components, which can then be recalled, modified, and synthesized at a later performance time. We have only considered half step and whole step transitions of the violin. We need to analyze transitions with larger pitch intervals and transitions with string changes. In general, more work has to be done on our violin synthesis, and more instruments have to be analyzed for their transition characteristics. With the advent of faster processing power, a more realistic synthesis technique will be available to the musician.

APPENDIX A. LEMUREDIT MANUAL

This appendix contains the distribution manual that accompanies LemurEdit. LemurEdit can be obtained via anonymous ftp from "unicorn.cerl.uiuc.edu" in the "/pub/lemur" directory.

LemurEdit(TM) 1.7 (2185)

A Graphical Editing Tool for Lemur(TM) Analyses

Written by Bryan Holloway (Homey@uiuc.edu)

CERL Sound Group

University of Illinois

Requirements:

LemurEdit requires a Mac II or greater with a FPU. The amount of memory needed is directly proportional to the size of the analysis files you want to load. 4MB is recommended for a one- to two-second analysis with lots of peak data. LemurEdit is known to run on System 6.0.5 or higher.

High gray-scale resolutions should be chosen in the Monitors section of the Control Panel since amplitude is represented by varying shades of gray.

Viewing a Lemur analysis:

LemurEdit allows the user to examine closely a Lemur analysis of a sound. Launching the application will show a quick splash page. Click the mouse or hit any key. You will then be prompted for a Lemur analysis file-name. After loading the file, you can zoom in on different regions of the graph. Use a click-and-drag operation to select a region of interest. Command-Z or selecting "Zoom" from the Actions menu will display a close-up of the selected region.

To reload a full-size version of the analysis, choose "Full Zoom Out" in the Edit Menu.

Multiple Lemur analyses can be open at the same time.

Amplitude scaling can be changed from a logarithmic scale to a linear scale from the Scaling menu. LemurEdit defaults to a logarithmic scale since it tends to show more amplitude detail.

Editing a Lemur analysis:

There are a number of operations that can be performed on a Lemur analysis. At any time you can save the file ("Save" in the File menu) to its original file-name, or use "Save As..." (in the File menu) to specify a new Lemur Analysis file. Saving is highly recommended since at this time there is no Undo option.

Saving selected tracks:

A check-box has been added to the standard "Save As..." dialog to allow the saving of ONLY selected tracks from an analysis. This feature is extremely useful in picking out portions of an analysis and saving them into different files. There are two ways to select tracks:

a) Manual track selection -- Simply clicking the mouse button will select the closest track in the vertical direction. If no track passes through the frame where the cursor is, no track will be selected.

b) Region track selection -- Select a region as if you were going to zoom. Press Command-S or choose "Select Tracks" from the Actions menu to select those tracks within the region. Press Command-D or choose "De-select Tracks" from the Actions menu to de-select those tracks. Press Command-T or choose "Toggle tracks" to turn off tracks that were previously on, and turn on tracks that were previously off. NOTE: As of this version, only tracks whose BIRTH lies within the region will be selected (or de-selected.) In other words, if a region does not enclose the birth of a track, it will NOT be selected, even if part of the track does lie within the region.

Time-Cutting:

Chunks of time can be removed from a Lemur analysis by selecting an appropriate region in time and hitting Command-X or selecting "Time-cut" from the Edit menu. LemurEdit will attempt to join both ends on either side of the cut as best as it can using the same parameters that the original Lemur analysis used, i.e. frequency drift.

Track Connection:

To join two tracks, select two tracks and press Command-C or choose "Connect Tracks" from the Edit Menu. Some restrictions are imposed upon track connections. First, you may not connect tracks that overlap in time. Second, if you try to connect tracks that could not be connected in Lemur due to the frequency-drift parameter of the analysis, LemurEdit will warn you, but still allow you to join them. Note that connecting two tracks does not change the analysis file on disk.

Labeling Peaks:

A 16-bit label field has been added to the peak structure. One can label these peaks and then use that information when doing one's own processing of Lemur analysis files. Peak labels do not have to be the same for a given track. To label peaks, select tracks OR a region and press Command-L or choose "Label Peaks" in the Actions Menu. This feature was added particularly for research purposes and may not otherwise be useful.

Playing a Lemur analysis in real time using the Capybara(TM):

This is part of work in progress and should only be used after consultation with the CERL Sound Group. If you have a Capybara, you can use a Sum-Of-Sines (SOS) Kyma sound to play back Lemur Analysis files in real time. Start Kyma and play the Setup sound that corresponds to the SOS-version of the analysis you are going to synthesize. Then launch LemurEdit, and load the Lemur Analysis version of the analysis. From the Options menu choose:

"Play" (Command-P) to play the selected tracks.

The Capybara will play the selected tracks and then loop back after reaching the end of the analysis. Press Command-K to stop playing.

Known bugs:

Occasionally when playing analysis files through the Capybara, the SOS program resident on the Capybara will hang. This can be remedied by replaying the Setup sound in Kyma.

APPENDIX B. ADVANCED DATA STRUCTURES USED IN LEMUREDIT

This appendix illustrates the advanced data types used in LemurEdit. Table B.1 is a description of the WindowSet structure that represents an analysis file and its graphs in memory. Table B.2 is a description of the LemurWindow structure that represents a particular region of an analysis displayed on the Macintosh screen. Table B.3 shows the header of a Lemur analysis file, and Figure B.1 is a block diagram illustrating the way in which frames and peaks are stored on disk.

Table B.1: WindowSet Structure.

Variable                    Comment                                              
firstLemurWin;              Pointer to linked-list of corresponding              
                            LemurWindows.                                        
parameters;                 Analysis Parameters for this WindowSet.              
firstFrame;                 Pointer to first frame in Lemur Analysis-file.       
listOfTracks;               Pointer to a linked-list of tracks selected by the   
                            user.                                                
trackTable;                 Pointer to a track-table structure.  This includes   
                            parameters used by the SOS protocol.                 
maximumAmplitude;           The loudest peak's amplitude within the entire       
                            analysis.  This value is used for plotting shades    
                            of gray to represent amplitude.                      
numberOfFrames;             Number of frames in this Analysis.                   
numberOfPeaks;              Number of peaks in this Analysis.                    
numberOfSelTrks;            Number of user-selected tracks.                      
lemurFileSpec;              Macintosh System 7 file data structure for this      
                            Analysis-file.                                       
lemurFileRefNum;            Macintosh File marker for accessing Analysis-file.   
numGraphs;                  The number of LemurWindows currently open with       
                            this WindowSet                                       
defGWidth;                  Default LemurWindow width (in pixels).               
defGHeight;                 Default LemurWindow height (in pixels).              
baseAddr;                   Pointer to base of Macintosh memory allocated for    
                            a WindowSet's frame and peak structures.             
currentAddr;                Pointer to current frames and peaks memory           
                            allocation address.                                  
TTbaseAddr;                 Pointer to base of Macintosh memory allocated for    
                            the WindowSet's Track-Table.                         
TTcurrAddr;                 Pointer to current Track-Table memory allocation     
                            address.                                             
protocolHandle;             Handle to external value that allows LemurEdit to    
                            talk to the Capybara using the SOS protocol.

Table B.1: WindowSet Structure (continued).

envRateHandle;              Handle to external value that controls the SOS       
                            sound's sample-increment.                            
triggerHandle;              Handle to external value that controls the SOS       
                            sound's trigger.                                     
whatAmIDoing;               Current state of this WindowSet (Idling, Graphing,   
                            etc.)                                                
regionRect;                 Macintosh QuickDraw coordinates of region selected   
                            by user.

Table B.2: LemurWindow Structure.

Variable                    Comment                                              
myWindow;                   Pointer to the Macintosh Window structure.           
offScreenPix;               Pointer to an off-screen bitmap of the current       
                            graph.                                               
gWidth;                     Width in pixels of this LemurWindow.                 
gHeight;                    Height in pixels of this LemurWindow.                
pixelToFrameRatio;          Number of pixels contained within one frame          
                            (fractional).                                        
mySubset;                   Structure describing the bounds on this              
                            LemurWindow in frames and frequency.                 
newSubset;                  Structure describing the bounds on a close-up in     
                            frames and frequency.                                
parent;                     Pointer to this LemurWindow's WindowSet.             
nextMQWin;                  Pointer to the next LemurWindow in this WindowSet.

Table B.3: Header, Frame and Peak Data of a Lemur Analysis File.

Variable                   Comment (units)                                      
analysisThreshold;         This parameter specifies the noise floor of the      
                           input signal.  Any peaks found below it are          
                           assumed to be noise (dB).                            
analysisRange;             This parameters specifies the local threshold for    
                           picking peaks.  Any peaks found below the            
                           magnitude of the loudest peak minus the local        
                           threshold are thrown out (dB).

Table B.3: Header, Frame and Peak Data of a Lemur Analysis File (continued).

hysteresis;                This parameter specifies the amount of hysteresis    
                           allowed for tracks.  It is the difference between    
                           the amplitude thresholds for the birth of a track    
                           and the continuation of a track (dB).                
mainLobeWidth;             This is a Kaiser window parameter for specifying     
                           side-lobe width of the window (Hz).                  
sidelobeAttenuation;       This is also a Kaiser window parameter for           
                           specifying side-lobe height (dB).                    
analysisFrameLength;       This parameter specifies the amount of time          
                           between consecutive frames (s).                      
originalNumSamples;        The total number of samples in the analysis.         
analysisSampleRate;        The sample-rate used during the analysis (Hz).       
frequencyDrift;            This analysis parameter specifies the relative       
                           amount of track frequency drift allowed over the     
                           duration of a frame (Hz percentage).

Figure B.1: Lemur File Structure [16].

APPENDIX C. THIRTY-TWO TRANSITIONS

This appendix describes the two sets of 16 digital violin recordings performed by Ms. Katherine Kim. Table C.1 describes the pitch interval, direction, and comments of each transition. Only one set is tabulated here, since the two sets were identical. Figures C.1 - C.32 are LemurEdit graphs of both sets of the corresponding Lemur analyses.

When analyzing the thirty-two transitions, the following analysis parameters were used: a -70 dB Noise floor, a 15 dB local threshold, 15 dB of hysteresis, and a 2% allowed frequency drift.

Table C.1: Two Sets of 16 Violin Transitions

   No.       Interval      Direction                 Comment                
1              Half-Step     Ascending  B to C on the A string (440 Hz),    
                                        slurred, notes are equal length     
2              Half-Step     Ascending  B to C, slurred, first note         
                                        longer than second                  
3              Half-Step     Ascending  B to C, slurred, first note very    
                                        long, 2nd note short                
4              Half-Step     Ascending  B to C, slurred, gritty attack,     
                                        first note shorter than second      
5              Half-Step    Descending  B to C, slurred, gritty attack,     
                                        both notes equal in length          
6             Whole-Step     Ascending  B to C# on A string, slurred,       
                                        notes equal length                  
7             Whole-Step    Descending  C# to B on A string, slurred,       
                                        notes equal length                  
8             Whole-Step     Ascending  Open A to B, vibrato on second      
                                        note                                
9             Whole-Step    Descending  B to Open A, slight vibrato on      
                                        first note, second note allowed     
                                        to ring                             
10             Half-Step     Ascending  B to C on A string, smooth, bow     
                                        change, slight vibrato on both      
                                        notes                               
11             Half-Step     Ascending  B to C, marcato, bow change         
12             Half-Step     Ascending  B to C, separated bow change,       
                                        accented                            
13             Half-Step     Ascending  B to C, slurred, no vibrato         
14             Half-Step     Ascending  B to C, slurred, no vibrato         
15             Half-Step    Descending  C to B, slurred, no vibrato         
16             Half-Step     Ascending  B to C on the A string, slurred,    
                                        notes are equal length

Transition Set A

Transition #1